・導体の代わりに仮想的に電荷を置いて考えるよ

影像電荷…何だっけ?
簡単に言うと
電気影像法とは
普通の方法では求められないような電界を求めるためのテクニック
です。
クーロンの法則やガウスの法則では簡単に解けない問題も、電気影像法を使えば解けてしまう場合があるのです。
今回の話は少し難しいです!

詳しく言うと
【ステップ1】電気影像法の目的
まず、そもそも電気影像法は何を求めるために作られた方法なのかお教えしましょう。
例えば、図のように空間上に点電荷$+Q$と無限に広い平面導体がある場合を考えましょう。
点電荷から出る電気力線は必ず導体と垂直になります。なぜなら、電界に平行成分があれば、導体表面の電荷が平行成分の力を受けて、平行成分がなくなるまで導体表面を移動するからです。
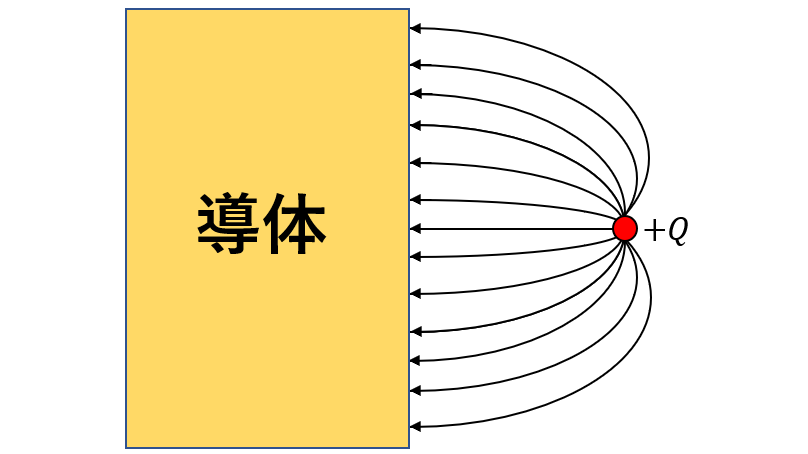
今、点電荷$+Q$周りの電界を求めたいのですが、どうやったら求めることが出来るでしょうか?クーロンの法則?ガウスの法則?いずれもうまく計算することはできません。導体が電界にどのような影響を及ぼしているか分からないのです。
そこで、点電荷$+Q$周りの電界を求めるために作られた方法こそが「電気影像法」なのです。
【ステップ2】電気影像法の理屈
さて、電気影像法を使って電界を求める道筋を説明していきます。
空間上に点電荷$+Q$と$-Q$があるとき、電界は$+Q$から$-Q$の方向にかかっています。それを電気力線で可視化すると図のようになります。
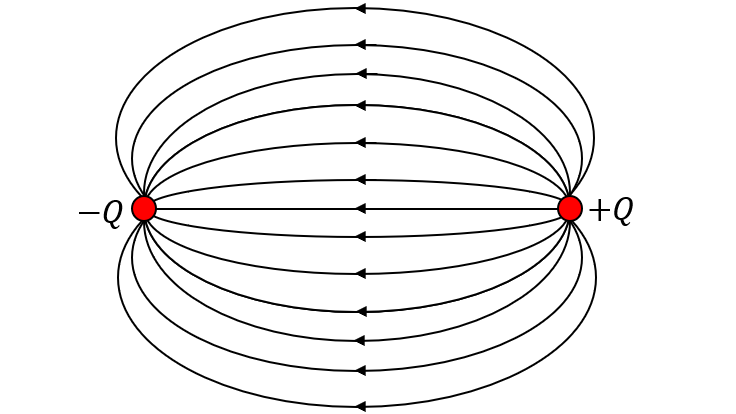
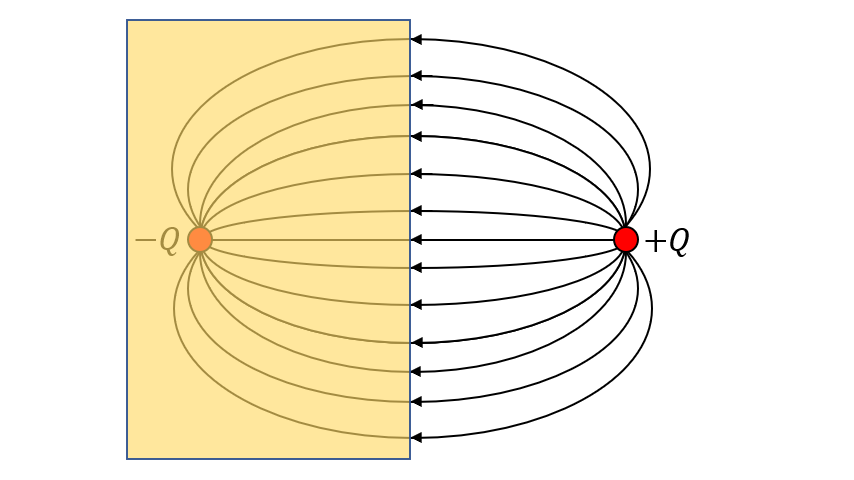
先ほどの図と見比べると、右半分が完全に同じ形になっていますよね?
つまり、導体がある場合でも、点電荷$-Q$がある場合でも、点電荷$+Q$周りの電界は変わらないのです。
そこで、図のように、$+Q$と真反対の位置にあたかも$-Q$があるかのように考え、クーロンの法則で電界を求めるというのが電気影像法の理屈です。
【ステップ3】電界を計算する
それでは点電荷周りの電界を求めてみましょう。点電荷と導体表面の距離を$d$として座標系を取り、点Pを適当に置きます。
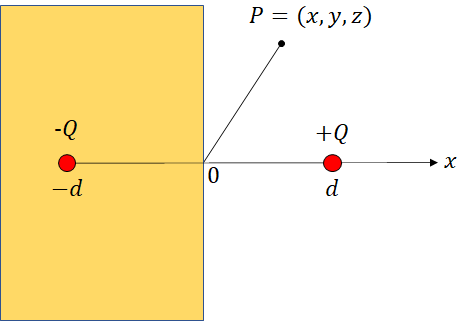
$\overrightarrow{ +QP } = (x-d, y, z)$、 $\overrightarrow{ -QP } = (x+d, y, z)$です。
$\hat{\mathbf{r}} = \frac{\mathbf{r}}{r}$であるので、クーロンの法則をこのように書き換えることが出来ます。
$$\mathbf{E}(\mathbf{r}) = \frac{Q}{4\pi\varepsilon_{0}r^2}\hat{\mathbf{r}} = \frac{Q}{4\pi\varepsilon_{0} r^3}\mathbf{r}$$
よって、
が、求めたかった電界です。
要するに何?
導体が電界に及ぼす影響が分からないから、代わりに点電荷を電気力線が同じ形になる位置に仮想的に置いて、クーロンの法則を使って電界を求める方法が「電気影像法」ってことですね~
お疲れ様でした!











初学者におすすめな参考書を調査してまとめてみました。良かったら参考にしてください。