文脈自由文法とは?
文脈自由文法(Contest-Free Grammar : CFG)とは「前後関係に依存せずに、非終端記号Aと非終端記号と終端記号の記号列αにおいて、$A \rightarrow alfa$という置換ができる文法」です。
文脈自由文法は$G=(V, \Sigma, R, S)$という形式で表されます。ただ、これは文脈自由文法がどんな要素から成り立っているかを示しているだけなので、読み飛ばしても構いません。
各記号の意味は以下の通りです。
・$G$:文脈自由文法の名前
・$V$:非終端記号の集合
・$\Sigma$:終端記号の集合
・$R$:生成規則
・$S$:開始記号
非終端記号、終端記号、生成規則、開始記号を例を使って説明します!

使用する記号などの説明
文脈自由文法は次のようなものです。
$$\begin{eqnarray}A &\rightarrow& aA\\
A &\rightarrow& B\\
B &\rightarrow& b \end{eqnarray}$$
非終端記号
矢印の左側にある$A, B$のことを非終端記号といい、その名の通り、最終的に導出される記号列には非終端記号があってはいけません。$aaaAb$みたいなのはダメってことです。
終端記号
非終端記号以外の記号$a,b$のことを終端記号といい、最終的に導出される記号列はこの終端記号だけで構成されていなければなりません。$aaaab$みたいなのはOKってことです
生成規則
$A \rightarrow aA, A \rightarrow B,B \rightarrow b$などの「非終端記号→非終端記号と終端記号の記号列」という文のことを生成規則といいます。
例えば、ある記号列$aA$に$A \rightarrow aA$を適用したとき、導出を表す記号「$\Rightarrow$」を使って、$aA \Rightarrow aaA$と書きます。
開始記号
文脈自由文法の最初の生成規則$A \rightarrow aA$の左側の非終端記号$A$のことを開始記号といいます。文字列の導出はこの記号から始める必要があり、いきなり$B \Rightarrow b$とすることはできません。
今回の例では、文脈自由文法$G=(V, \Sigma, R, S)$は次のように書くことが出来ます。

$$\begin{eqnarray} G &=& (V, \Sigma, R, S) \\
&=& ( \{ A,B \}, \{ a,b \}, \{ A \rightarrow aA | B, B \rightarrow b \}, \{A \}) \end{eqnarray}$$
文脈自由文法が生成する記号列
さて、先ほどの文脈自由文法が生成する記号列はどのようになるでしょうか?
$$\begin{eqnarray}A &\rightarrow& aA\\
A &\rightarrow& B\\
B &\rightarrow& b \end{eqnarray}$$
まずは、適当に生成規則を使って記号列を生成してみましょう。
$$\begin{eqnarray} A \Rightarrow aA &\Rightarrow& aB \Rightarrow ab \\
A \Rightarrow aA &\Rightarrow& aaA \Rightarrow aaB \Rightarrow aab \\
A \Rightarrow aA &\Rightarrow& aaA \Rightarrow aaaA \Rightarrow aaaB \Rightarrow aaab \end{eqnarray}$$
生成する記号列は正規表現を使って表され、この文脈自由文法は$a^nb(n \geq 1)$という記号列を生成するだろうと推測できます。
生成する記号列は証明などはする必要がなく、「まぁ多分こういう記号列になるだろう」ぐらいの気持ちで大丈夫です。
文脈自由文法ではどんな記号列が生成できるかというのが最も大切なので、生成する記号列を求めることが出来るようにしておきましょう。

記号列を導出する
例えば、「記号列$aaab$を導出しなさい」という問題を考えましょう。使う文法は先ほどの例です。
こういう問題はとにかく、指定されている記号列になるように生成規則をうまく適用していけば良く、今回の例では以下のようになります。
$$A \Rightarrow aA \Rightarrow aaA \Rightarrow aaaA \Rightarrow aaaB \Rightarrow aaab$$
生成規則は1つ1つ順番に適用しましょう。つまり、$A \Rightarrow aA \Rightarrow aaA$を$A \Rightarrow aaA$と省略して書くのはダメってことです。テストでやったら減点されます。
では、記号列$aaab$の導出を構文木で表してみましょう。構文木とは導出仮定を視覚的に分かりやすく表したもので、開始記号から下向きに作ります。
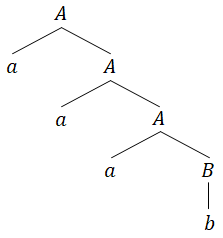
例題
(1)
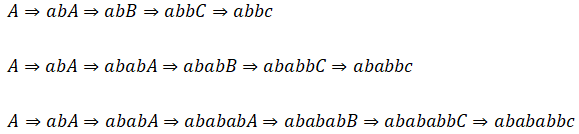
となるので、導出される記号列は$(ab)^n bc(n \geq 1)$である。
(2)
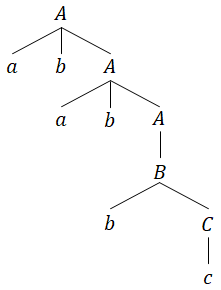








以下の文脈自由文法Gを考える。
$$\begin{eqnarray}A &\rightarrow& abA\\
A &\rightarrow& B \\
B &\rightarrow& bC \\
C &\rightarrow& c \end{eqnarray}$$
(1) Gが生成する記号列を正規表現で表しなさい
(2) 記号列$ababbc$の導出過程を構文木で示しなさい。