今回のポイント
・電荷分布から電位を求めるための方程式だよ
・ガウスの法則をちょっといじっただけだよ
くるる
むぅ…なんか難しそうっすね…
簡単に言うと
ポアソンの方程式とは
電荷の分布が分かれば、電位を求めることができる魔法の方程式
です。
このポアソンの方程式を用いて電位を求め、そこから電界を求めるというのが、電界を求める一般的なルートなのです。
詳しく見ていきましょう！
先生
詳しく言うと
ポアソンの方程式は
$$∆V(\mathbf{r}) = -\frac{\rho(\mathbf{r})}{\varepsilon_{0}}$$
という形で書かれます。これを導出していきましょう。
まずはガウスの法則（微分形）からスタートします。ガウスの法則（微分形）は
$$∇ \cdot \mathbf{E}(\mathbf{r}) = \frac{\rho(\mathbf{r})}{\varepsilon_{0}}$$
でした。また、電界と電位には
$$\mathbf{E}(\mathbf{r}) = -∇V(\mathbf{r})$$
という関係があります。下の式を上の式に代入してみましょう。すると、
$$∇ \cdot ∇V(\mathbf{r}) = ∆V(\mathbf{r}) = -\frac{\rho(\mathbf{r})}{\varepsilon_{0}}$$
というように導出が出来ました。
そして、導出の仕方から分かるように、ポアソンの方程式とは、ガウスの法則を変形させただけのものなのです
だから、ポアソンの方程式と聞くと、何やら得体の知れない難しい方程式なのかと思うかもしれませんが、その実態はただガウスの法則をちょっといじっただけのものと考えれば簡単に受け入れることが出来るのではないでしょうか。
名前は難しそうですが、実際大したことありません。
先生
ガウスの法則について詳しく知りたい方は「ガウスの法則のイメージや導出を分かりやすく解説！」をご覧ください。
例題
では実際にポアソンの方程式を使って例題を解いてみましょう。
図のように、面積$S$、距離$d$の平行平板導体間に電荷密度$\rho$で電荷が一様に分布している。平行平板の片方を接地し、もう片方の電位を$V$としたときの平行平板導体間におけるx方向の電位の分布を求めよ。
解答
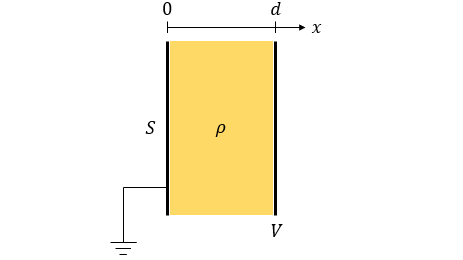
要するに何？
ガウスの法則をちょっといじって、電荷分布から電位分布を求められるようにしたものが、ポアソンの方程式ってことです(^^♪
今回はこんな感じ(‘ω’)ノ
ポアソンの方程式より、
$$∆V(\mathbf{r}) = -\frac{\rho}{\varepsilon_{0}}$$
$∆ = (\frac{\partial^2}{\partial x^2} + \frac{\partial^2}{\partial y^2} + \frac{\partial^2}{\partial z^2})$であるので、
$$(\frac{\partial^2}{\partial x^2} + \frac{\partial^2}{\partial y^2} + \frac{\partial^2}{\partial z^2})V(\mathbf{r}) = -\frac{\rho}{\varepsilon_{0}}$$
となります。そして$x$方向の電位を求めたいので、
$$\frac{\partial^2 V(x)}{\partial x^2} = -\frac{\rho}{\varepsilon_{0}}$$
$V(x)$は$x$成分しか持ちませんので、$\partial$を$d$に変えてしまいましょう。
$$\frac{d^2 V(x)}{dx^2} = -\frac{\rho}{\varepsilon_{0}}$$
両辺$x$で積分すると、
$$\frac{dV(x)}{dx} = -\frac{\rho}{\varepsilon_{0}}x + C_{1}$$
もう1回積分すると
$$V(x) = -\frac{\rho}{2\varepsilon}x^2 + C_{1}x + C_{2}$$
初期条件$V(0) = 0$より$C_{2} = 0$、$V(d) = V$より$C_{1} = \frac{V}{d} + \frac{\rho d}{2\varepsilon_{0}}$と求まるので、
$$V(x) = -\frac{\rho}{2\varepsilon}x^2 + (\frac{V}{d} + \frac{\rho d}{2\varepsilon_{0}})x$$
です！