導入
さて、コーシーリーマンの関係式の説明を始める前に、まずは「なぜコーシーリーマンの関係式というものを考えるのか」を説明しましょう。
今回の目的
今回の目的はずばり、「関数$f(z)$が点$z$で微分可能かどうかを調べること」です。$z$はもちろん$z=x+iy$で表される複素数ですよ。

それがコーシーリーマンの関係式?というやつとどう関係してるんすか?
関数$f(z)$が点$z$においてコーシーリーマンの関係式を満たすならば、$f(z)$は点$z$で微分可能であると言えるのです!

では、「点$z$で微分可能」であるためには、最低でもどのような条件は満たしていなければいけないかを考えましょう。
点$z$で微分可能であるために最低限満たすべき条件
複素数の世界での「微分可能」は、実数の世界での「微分可能」とは少し違うものでした。
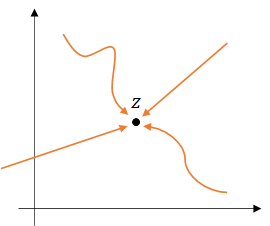
上図のように点$z$に近づくあらゆる経路において、導関数
$$f'(z) = \displaystyle \lim_{ \Delta z \to 0 } \frac{f(z+\Delta z)-f(z)}{\Delta z}$$
が同じ値に収束しなければなりません。それが、複素数の世界での「微分可能」の条件でした。
しかし、本当にあらゆる経路における導関数を求めるのは無理な話です。そこで、以下の図のように、$+x$方向から近づく経路と、$+y$方向から近づく経路の2つを考えましょう。
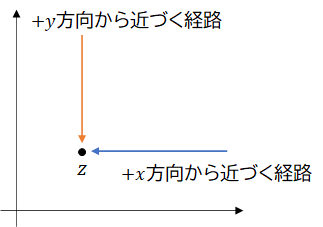
「$+x$方向と$+y$方向から近づく経路における導関数が同じ値に収束する」というのが、点$z$において微分可能であるために最低限必要な条件です。
それでは、コーシーリーマンの関係式の説明に入ります!

コーシーリーマンの関係式
先にコーシーリーマンの関係式とはどういうものなのか見てもらいましょう。次のようなものです。
関数$f(z) = u(x,y)+iv(x,y)$が点$z$で微分可能ならば、
$$\frac{ \partial u }{ \partial x } = \frac{ \partial v }{ \partial y }$$
$$\frac{ \partial v }{ \partial x } = -\frac{ \partial u }{ \partial y }$$
であり、この2式をコーシーリーマンの関係式という。また、このときの導関数は次の式で与えられる。
$$f'(z) = \frac{ \partial u }{ \partial x }+i\frac{ \partial v }{ \partial x } = -i\frac{ \partial u }{ \partial y }+\frac{ \partial v }{ \partial y }$$
つまり、簡単に言えば、

という定理です。

な、なんだか、難しそうだね…
この定理を証明します!

証明
定理は「関数$f(z) = u(x,y)+iv(x,y)$が点$z$で微分可能ならば、」という文から始まっています。先ほど、「点$z$で微分可能であるために最低限満たすべき条件」を説明しましたよね?それを利用するのです。
つまり、コーシーリーマンの関係式の定理は
関数$f(z) = u(x,y)+iv(x,y)$が点$z$で微分可能ならば、点$z$に$+x$方向, $+y$方向から近づく経路における導関数が同じ値に収束するはず
というアイデアのもと生まれた定理なわけです。それでは2つの経路における導関数を求めてみましょう。導関数の式は以下の通りです。
$$f'(z) = \displaystyle \lim_{ \Delta z \to 0 } \frac{f(z+\Delta z)-f(z)}{\Delta z}$$
また、$z=x+iy$, $\Delta z=\Delta x+i\Delta y$という関係から、
$$f(z+\Delta z) = u(x+\Delta x, y+\Delta y)+iv(x+\Delta x, y+\Delta y)$$
となることも理解しておいてください。
$+x$方向から近づく経路における導関数
$+x$方向から近づくとき、$\Delta y = 0$で$x$だけが変化するので、導関数の式における$\Delta z \rightarrow 0$は$\Delta x \rightarrow 0$と等しくなります。
導出は以下の通りです。

$+y$方向から近づく経路における導関数
$+x$方向から近づくとき、$\Delta x = 0$で$y$だけが変化するので、導関数の式における$\Delta z \rightarrow 0$は$\Delta y \rightarrow 0$と等しくなります。
導出は以下の通りです。

証明のまとめ
$f(z)$の$+x$方向と$+y$方向から近づく経路の導関数$f'(z)$はそれぞれ次のようなものだと分かりました。
$$\frac{ \partial u }{ \partial x }+i\frac{ \partial v }{ \partial x }$$
$$-i\frac{ \partial u }{ \partial y } = \frac{ \partial v }{ \partial y }$$
そして、この2つの導関数が等しくなくてはいけないわけです。したがって、実部と虚部をそれぞれ比較して、
$$\frac{ \partial u }{ \partial x } = \frac{ \partial v }{ \partial y }$$
$$\frac{ \partial v }{ \partial x } = -\frac{ \partial u }{ \partial y }$$
という2式が成り立ち、この2式こそが「コーシーリーマンの関係式」です。
また、導関数の式ですが、$f(z)$の$+x$方向と$+y$方向から近づく経路の導関数$f'(z)$が等しいわけですから、
$$f'(z) = \frac{ \partial u }{ \partial x }+i\frac{ \partial v }{ \partial x } = -i\frac{ \partial u }{ \partial y }+\frac{ \partial v }{ \partial y }$$
となるのも当然ですよね。
証明は以上です!

今回のまとめ
・関数$f(z)$が点$z$で微分可能 = 点$z$でコーシーリーマンの関係式が成り立つ
・コーシーリーマンの関係式
$$\frac{ \partial u }{ \partial x } = \frac{ \partial v }{ \partial y } \quad \frac{ \partial v }{ \partial x } = -\frac{ \partial u }{ \partial y }$$
・コーシーリーマンの関係式が成り立つときの導関数
$$f'(z) = \displaystyle \lim_{ \Delta z \to 0 } \frac{f(z+\Delta z)-f(z)}{\Delta z}$$












・関数$f(z)$が点$z$で微分可能 = 点$z$でコーシーリーマンの関係式が成り立つ
・コーシーリーマンの関係式
$$\frac{ \partial u }{ \partial x } = \frac{ \partial v }{ \partial y } \quad \frac{ \partial v }{ \partial x } = -\frac{ \partial u }{ \partial y }$$
・コーシーリーマンの関係式が成り立つときの導関数
$$f'(z) = \displaystyle \lim_{ \Delta z \to 0 } \frac{f(z+\Delta z)-f(z)}{\Delta z}$$