複素積分とは?

う~ん。複素積分ってのを授業で習ったけど、いまいち何を求めているのかよく分からないなぁ…
簡単に説明しましょう!

複素積分は線積分
まず、しっかり覚えておいてほしいのですが、複素積分は「線積分」です。普通の積分と思ってると意味が分からなくなるので注意しましょう。
複素積分は次のような記法で表されます。$z$は複素数、$C$は積分経路です。
$$\displaystyle \int_{C} f(z) dz$$
さて、積分経路$C$が次のようなものであったとしましょう。
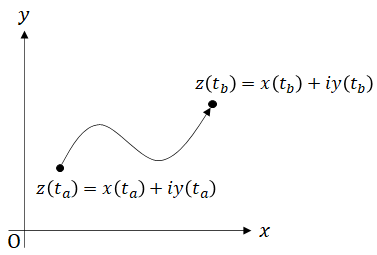
このとき、積分経路$C$は次のような式で表すことができます。
$$z(t) = x(t)+iy(t) \quad (t_a \leq t \leq t_b)$$
すると、複素積分の式は次のように変形することができます。
$$\begin{eqnarray} \displaystyle \int_{C} f(z) dz &=& \displaystyle \int_{t_a}^{t_b} f(z(t)) dz(t) \\ &=& \displaystyle \int_{t_a}^{t_b} f(z(t)) \frac{dz(t)}{dt} dt \end{eqnarray}$$
この変形が凄く重要です!

例題で理解を深めよう
簡単な例題を使って、複素積分に対する理解を深めていきましょう。
積分経路$C$が$z = 2ti \ (0 \leq t \leq 1)$で表されるとき、次の複素積分を求めよ。
$$\displaystyle \int_{C} z^2 dz$$
$z = 2ti \ (0 \leq t \leq 1), \frac{dz}{dt} = 2i$より
$$\begin{eqnarray} \displaystyle \int_{C} z^2 dz
&=& \displaystyle \int_{0}^{1} (2ti)^2 \cdot 2idt \\
&=& \displaystyle \int_{0}^{1} -8it^2 dt \\
&=& -8i \left[ \frac{1}{3}t^3 \right]_0^1 \\
&=& -\frac{8}{3}i \end{eqnarray}$$
複素積分のイメージ

複素積分って結局何を求めてるのかがイメージできないんっすよね…
線積分をしっかり理解することが大切です!

複素積分はあくまでも線積分です。$f(z(t))$という関数の$z(t)$だけを積分経路$C$に沿って変化させたときの$f(z(t))$の和を求めているわけです。
例えば、$z(t)$が直線だとすると、次のようなイメージになります。$z(t)$と$f(z(t))$に囲まれた部分の面積が複素積分の積分値です。
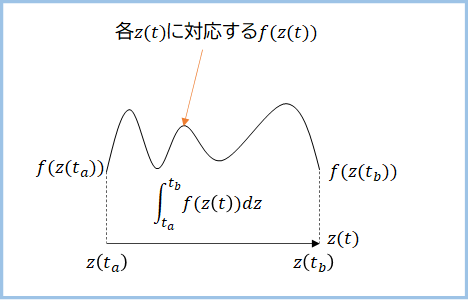
2次元でイメージするなら次のような感じ。

$z(t)$の積分ではなく、$f(z(t))$の積分をしているのだときちんと理解しましょう。

今回のまとめ
・複素積分は線積分
・以下の変形が大事
$$\begin{eqnarray} \displaystyle \int_{C} f(z) dz = \displaystyle \int_{t_a}^{t_b} f(z(t)) \frac{dz(t)}{dt} dt \end{eqnarray}$$
・複素積分は$f(z(t))$という関数の$z(t)$だけを積分経路$C$に沿って変化させたときの$f(z(t))$の和を求めている












・複素積分は線積分
・以下の変形が大事
$$\begin{eqnarray} \displaystyle \int_{C} f(z) dz = \displaystyle \int_{t_a}^{t_b} f(z(t)) \frac{dz(t)}{dt} dt \end{eqnarray}$$
・複素積分 = $f(z(t))$という関数の$z(t)$だけを積分経路$C$に沿って変化させたときの$f(z(t))$の和の計算