留数とは?
留数とは簡単に言えば、「線積分しても$0$にならずに残る部分」です。
例えば、次のような式を考えましょう。
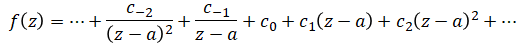
これは、ある関数$f(z)$がローラン展開された後の式です。
今、この式を適当な閉曲線$C$に沿って線積分したいのですが、項が無限にあり、普通の複素積分では求めるのが難しそうですよね?
でも、実は上記の線積分の結果は次のような式で求めることが出来るのです。
$$\displaystyle \int_{C} f(z) dz = 2\pi i \cdot c_{-1}$$
この式の導出は以下の通りです。
以下のような線積分を考える。
$$\displaystyle \int_{C}(z-a)^n dz$$
$z-a=re^{i\theta} \ (0 \leq \theta \leq 2\pi)$とおくと、$dz=ire^{i\theta}d\theta$であるから、
$$\begin{eqnarray}
\displaystyle \int_{C}(z-a)^n dz
&=& \displaystyle \int_{0}^{2\pi} r^n e^{in\theta} \cdot ire^{i\theta}d\theta \\
&=& ir^{n+1} \displaystyle \int_{0}^{2\pi} e^{i(n+1)\theta} d\theta \\
&=& ir^{n+1} \displaystyle \int_{0}^{2\pi} \{cos(n+1)\theta+isin(n+1)\theta \} d\theta \\
&=& \begin{cases} 2\pi i & ( n=-1 ) \\ 0 & ( n \neq -1 ) \end{cases}
\end{eqnarray}$$
したがって、$f(z)$の線積分は$\frac{c_{-1}}{z-a}$の項以外は全て$0$になるため、
$$\displaystyle \int_{C} f(z) dz = 2\pi i \cdot c{-1}$$
このとき、$c_{1}$のことを線積分しても消えずに留まっている数という意味で「留数」と言います。特に、特異点が$z=a$であるため、「$z=a$における留数」ともいわれます。また、留数は英語でResidueと書くので、$Res[a]$という記号で表されることが多いです。後でこの記号を使うので、覚えておいてください。

つまり、どういうことっすか?
ローラン展開の形の式ならば、線積分するとどんな式でも$2\pi i \cdot c_{-1}$という値になるということです!

元々$f(z)$を閉曲線$C$に沿って線積分するのが目標であったため、$c_{-1}$さえ求まれば、積分値は$2\pi i \cdot c_{-1}$と分かります。
しかし、ここで問題になるのが、「どうやって$c_{-1}$を求めるか?」ということです。最初からローラン展開の形の式になっていれば$c{-1}$はすぐに求まりますが、大体は$f(z)$をローラン展開しないといけません。
でも、$c_{-1}$だけあればいいのに、わざわざローラン展開するのも面倒ですよね?
そこで、留数$c_{-1}$だけを求める超便利な方法があるのです。
留数の求め方
留数の求め方は「点$a$が$1$位の極のとき」と「点$a$が$k$位の極のとき」の2パターン存在します。
この「~位の極」という言葉の意味について、まず簡単に説明します。
極について
例えば、ある関数$f(z)$のローラン展開が次のような式になっていたとします。
$$f(z)=\frac{c_{-1}}{z-a}+c_0+c_1(z-a)+c_2(z-a)^2+ \cdots$$
このとき、$a$は特異点で、$(z-a)^{-1}$の項から始まっているので、$a$のことを「$1$位の極」と言います。
次のような式なら、$a$は「$2$位の極」です。
$$f(z)=\frac{c_{-2}}{(z-a)^2}+\frac{c_{-1}}{z-a}+c_0+c_1(z-a)+c_2(z-a)^2+ \cdots$$
そして、一般的に、次のような$(z-a)^{-k}$の項から始まるとき、$a$を「$k$位の極」と言います。
$$f(z)=\frac{c_{-k}}{(z-a)^k}+ \cdots +\frac{c_{-1}}{z-a}+c_0+c_1(z-a)+ \cdots$$
とりあえず、そういう名前が付いているのだと理解するだけでOKです。

点$a$が$1$位の極のとき
さて、先ほどの「極」の説明より、点$a$が$1$位の極のときというのは、$f(z)$が次のような式にローラン展開できるということを示しています。
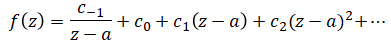
そして、この式において留数$c_1$を求めるのが目的ですが、点$a$が$1$位の極のときは結構簡単で、次のような計算式で求めることが出来ます。
$$Res[a]=\displaystyle \lim_{ z \to a } (z-a)f(z)$$
この式の証明は次のようになります。
点$a$が$1$位の極のとき$f(z)$は次のような式にローラン展開できる。
$$f(z)=\frac{c_{-1}}{z-a}+c_0+c_1(z-a)+c_2(z-a)^2+ \cdots$$
この式において、両辺に$(z-a)$を掛けると、
$$(z-a)f(z)=c_{-1}+c_0(z-a)+c_1(z-a)^2+c_2(z-a)^3+ \cdots$$
よって、両辺極限を取ると、
$$\displaystyle \lim_{ z \to a } (z-a)f(z)=c_{-1}=Res[a]$$
この方法であれば、すぐに留数を求めることが出来ますよね?面倒くさいローラン展開をしなくても済みます。

こんな簡単な式で求められるんだ!
点$a$が$k$位の極のとき
点$a$が$k$位の極のときというのは、$f(z)$が次のような式にローラン展開できるということを示しています。
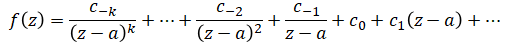
そして、点$a$が$k$位の極のときの留数は次のような計算式で求めることが出来ます。
$$Res[a]=\frac{1}{(k-1)!} \displaystyle \lim_{ z \to a } \frac{d^{k-1}}{dz^{k-1}} \{ (z-a)^k f(z) \} $$
この式の証明は次のようになります。
点$a$が$k$位の極のとき$f(z)$は次のような式にローラン展開できる。
$$f(z)=\frac{c_{-k}}{(z-a)^k}+ \cdots +\frac{c_{-1}}{z-a}+c_0+c_1(z-a)+ \cdots$$
両辺に$(z-a)^k$を掛けると、
$$(z-a)^k f(z)=c_{-k}+ \cdots +c_{-1}(z-a)^{k-1}+c_0(z-a)^{k}+c_1(z-a)^{k+1}+ \cdots$$
ここで、両辺を$(k-1)$回微分すれば、$c_{-1}(z-a)^{k-1}$以降の項だけが残るから、
$$\frac{d^{k-1}}{dz^{k-1}} \{ (z-a)^k f(z) \} =(k-1)!c_{-1}(z-a)+\frac{k!}{1!}c_0(z-a)+\frac{(k+1)!}{2!}c_1(z-a)^2+ \cdots$$
よって、両辺の極限を取ると
$$\frac{1}{(k-1)!} \displaystyle \lim_{ z \to a } \frac{d^{k-1}}{dz^{k-1}} \{ (z-a)^k f(z) \} =c_{-1}= Res[a]$$
この式は「点$a$が$1$位の極のとき」よりもかなりややこしい式になっていますが、大きくても$k=3$ぐらいなので、そこまで大変な計算ではありません。
以上が留数の求め方の説明で、この2つの計算方法を用いて留数を求めることで、$f(z)$の閉曲線$C$に沿った線積分の値が、
$$\displaystyle \int_{C} f(z) dz = 2\pi i \cdot c_{-1}$$
という式で求められます。

なんとなく分かったっす!
今回のまとめ
・留数は「線積分しても$0$にならずに残る部分」
・「$z=a$における留数」を$Res[a]$と書く
・留数の求め方は以下の2パターン
点$a$が$1$位の極のとき
$$Res[a]=\displaystyle \lim_{ z \to a } (z-a)f(z)$$
点$a$が$k$位の極のとき
$$Res[a]=\frac{1}{(k-1)!} \displaystyle \lim_{ z \to a } \frac{d^{k-1}}{dz^{k-1}} \{ (z-a)^k f(z) \}$$












・留数は「線積分しても$0$にならずに残る部分」
・「$z=a$における留数」を$Res[a]$と書く
・留数の求め方は以下の2パターン
点$a$が$1$位の極のとき
$$Res[a]=\displaystyle \lim_{ z \to a } (z-a)f(z)$$
点$a$が$k$位の極のとき
$$Res[a]=\frac{1}{(k-1)!} \displaystyle \lim_{ z \to a } \frac{d^{k-1}}{dz^{k-1}} \{ (z-a)^k f(z) \} $$