コーシーの積分公式とは?
話のスタート地点
いきなりコーシーの積分公式の説明をしても何が何やらだと思うので、まずはコーシーの積分公式が求められるに至った経緯をお話ししましょう。


お願いしますっす!
さて、この記事を見ている方はすでに「コーシーの積分定理」というものを知っていると思います。
コーシーの積分定理とは「領域$D$内の全ての$z$において$f(z)$が正則ならば、閉曲線$C$に沿った$f(z)$の線積分の値が$0$になるよ嬉しいね」という定理です。
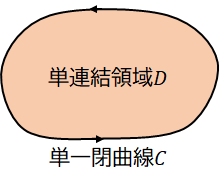
では、単連結領域$D$の内部に特異点がある場合を考えましょう。例えば、$f(z) = \frac{g(z)}{z-a}$という関数の場合、$z=a$が特異点になります。$g(z)$は$C$の内部で正則な関数で、$g(z)=z$なら$f(z) = \frac{z}{z-a}$です。
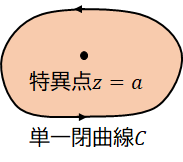
これでは「領域$D$内の全ての$z$において$f(z)$が正則」という条件を満たさないので、コーシーの積分定理は使えませんよね。
そして、このような「領域$D$の内部に特異点がある場合の閉曲線$C$に沿った線積分」を求めたい!というのが、今回の話のスタート地点です。
コーシーの積分公式が求まるまでの過程
「領域$D$の内部に特異点がある場合の閉曲線$C$に沿った線積分を求める」という目的を達成しにいきましょう。
まず、「特異点が邪魔なんだったら、取り除いてしまえ」ということで、次の図のように変形してしまいます。反時計回りを正としているため$-C’$になっています。
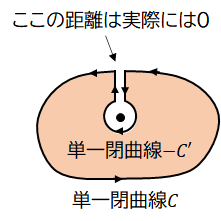
すると、この図の赤色の部分では$f(z) = \frac{g(z)}{z-a}$は正則であるため、コーシーの積分定理より、
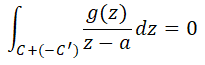
となります。この式より、次の式が容易に導けます。
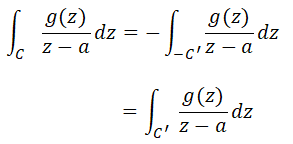
この式は「閉曲線$C$に沿った線積分=特異点周りの閉曲線$C’$に沿った線積分」になるということを表しています。

さて、元々の目的は「単連結領域$D$の内部に特異点がある場合の閉曲線$C$に沿った線積分を求める」だったので、この式の右辺の値が求まれば、この目的は達成されます。
そのために、以下の図のように、閉曲線の向きを変えて、閉曲線$C’$の作る円の半径を$r$、中心を$a$とします。
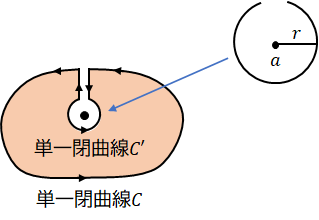
すると、$z=a+re^{i\theta}$と表されることから、次のような式が得られます。
$$z-a=re^{i\theta}, \ \frac{dz}{d\theta} = ire^{i\theta}$$
これを使って、先ほどの式の右辺を計算していきます。
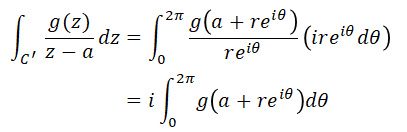
ここで、$r$は実際には極限まで小さくできます。つまり、$r \rightarrow 0$と出来るわけです。すると、
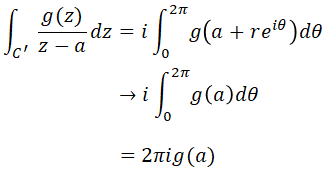
となりました。よって、目標にしていた右辺の式が求まったので、次の式が成り立ちます。
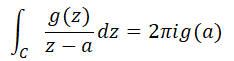
元々の目的は「単連結領域$D$の内部に特異点がある場合の閉曲線$C$に沿った線積分を求める」ことでしたが、色々計算した結果、このような式で求められると分かりました。
一般的には$g$を$f$にした次の形で使われています。
$$\displaystyle \int_{C} \frac{f(z)}{z-a} dz = 2 \pi if(a)$$
そして、この式のことを「コーシーの積分公式」と名付けたのです。


なるほどっす!
例題
実際にちゃんと求められるのか試してみましょう。
積分経路$C$が円$|z|=3$のとき、次の積分を求めよ。
$$\displaystyle \int_{C} \frac{z}{z-2i} dz$$
$f(z)=z$は$C$の内部及び$C$上で正則で、$z=2i$は$C$内部の点であるから、コーシーの積分公式より、
$$\displaystyle \int_{C} \frac{z}{z-2i} dz = 2 \pi if(2i) = 2 \pi i \cdot 2i = -4 \pi$$

という感じで、内部に特異点がある線積分の値を求めることが出来ました。
そして、今回の求めたコーシーの積分公式を使うと、複素数のテイラー展開とローラン展開というものが出来るようになるのです。
今回のまとめ
・コーシーの積分公式は「単連結領域$D$の内部に特異点がある場合の閉曲線$C$に沿った線積分を求める」ことが出来る公式
$$\displaystyle \int_{C} \frac{f(z)}{z-a} dx = 2 \pi if(a)$$
・コーシーの積分公式を使うと、複素数のテイラー展開とローラン展開というものが出来るようになる












・コーシーの積分公式は「単連結領域$D$の内部に特異点がある場合の閉曲線$C$に沿った線積分を求める」ことが出来る公式
$$\displaystyle \int_{C} \frac{f(z)}{z-a} dx = 2 \pi if(a)$$
・コーシーの積分公式を使うと、複素数のテイラー展開とローラン展開というものが出来るようになる