コーシーの積分定理とは?
コーシーの積分定理とは一言で言えば「閉曲線$C$に沿った$f(z)$の線積分の値が$0$になるよ嬉しいね」という定理です。
簡単に説明しましょう。
簡単な説明
例えば、次のような図を考えましょう。
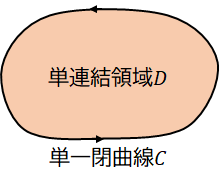
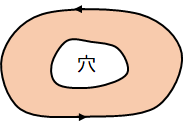
ここで、単連結領域とは「穴の開いていない領域」のことで、次の図のような領域は単連結領域ではありません。
また、単一閉曲線とは「交わりのない閉曲線」のことで、次の図のような閉曲線は単一閉曲線ではありません。
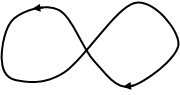
そして、ある複素関数$f(z)$の単一閉曲線$C$に沿った線積分
$$\displaystyle \int_{C} f(z) dz$$
を行うのですが、もし単連結領域$D$内で$f(z)$が正則ならば、
$$\displaystyle \int_{C} f(z) dz = 0$$
になるというのが、「コーシーの積分定理」です。なんとなく伝えることを目的としているので、この記事では証明はしません。
直感的なイメージ

何だか良く分からないので、直感的にどういう定理なのか説明してほしいです…
なんとなく説明しましょう!

まず、次のような図を考えます。

次に、「線積分の値が経路に依存しない」と仮定すると、次のような式が成り立ちます。
$$\displaystyle \int_{C_1} f(z) dz = \displaystyle \int_{C_2} f(z) dz$$
そして、曲線$C_2$の向きを逆にします。
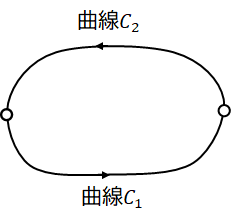
このとき、次のような式が成り立ちます。
$$\displaystyle \int_{C_1} f(z) dz = -\displaystyle \int_{C_2} f(z) dz$$
この式より、
$$\displaystyle \int_{C_1} f(z) dz + \displaystyle \int_{C_2} f(z) dz = 0$$
となり、曲線$C_1,C_2$をまとめて、曲線$C$と書くことにすると、
$$\displaystyle \int_{C} f(z) dz = 0$$
となります。この式がまさにコーシーの積分定理で成り立つ式ですよね?

なるほど、なるほど、、、
そして、途中で「線積分の値が経路に依存しない」と仮定しましたが、この仮定が成り立つ条件が、
単一閉曲線$C$かつ単連結領域$D$内で$f(z)$が正則

というわけです。逆に言えば、「コーシーの積分定理が成り立つ」=「線積分の値が経路に依存しない」と言えるのです。
直感的にはこんなイメージです。

コーシーの積分定理は何に役立つのか?

コーシーの積分定理が成り立つのは分かったっすけど、これが成り立つと何かの役に立つんすか??
領域$D$内に特異点があっても積分の計算が簡単にできるようになります!

例えば、次のように単一閉曲線$C$内に特異点がある状況を考えましょう。特異点は簡単に言えば「微分可能でない点」で、関数$\frac{1}{z}$の場合、$z=0$が特異点です。要は関数の値がおかしくなる点ですね。
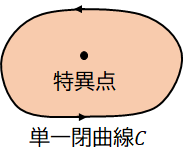
この場合コーシーの積分定理は使えません。「単連結領域$D$内で$f(z)$が正則」という条件が満たされないからです。
そこで次のように特異点を取り除くような図に変えてしまいましょう。

このとき、次のような式が成り立ちます。
$$\displaystyle \int_{C} f(z) dz = \displaystyle \int_{C’} f(z) dz$$
このように、コーシーの積分定理を使うと、単一閉曲線$C$に沿った線積分を特異点周りの単一閉曲線$C’$に沿った線積分に置き換えることが出来るのです。

ちゃんとした証明はここではしませんが、感覚的にはこんな感じです。
今回のまとめ
・コーシーの積分定理
単一閉曲線$C$の内部の単連結領域$D$において$f(z)$が正則のとき、次の式が成り立つ。
$$\displaystyle \int_{C} f(z) dz = 0$$
・単連結領域は「穴の開いていない領域」、単一閉曲線は「交わりのない閉曲線」
・コーシーの積分定理が成り立つ = 線積分の値が経路に依存しない
・コーシーの積分定理を使うと、領域$D$内に特異点があっても積分の計算が簡単にできる












・コーシーの積分定理
単一閉曲線$C$の内部の単連結領域$D$において$f(z)$が正則のとき、次の式が成り立つ。
$$\displaystyle \int_{C} f(z) dz = 0$$
・単連結領域は「穴の開いていない領域」、単一閉曲線は「交わりのない閉曲線」
・コーシーの積分定理が成り立つ = 線積分の値が経路に依存しない
・コーシーの積分定理を使うと、領域$D$内に特異点があっても積分の計算が簡単にできる