留数定理とは?
留数定理とは「閉曲線$C$に沿った周回線積分の値が、$C$内部の全ての 孤立特異点における留数の和に$2\pi i$をかけたものになる」という定理で、次のような公式で表されます。
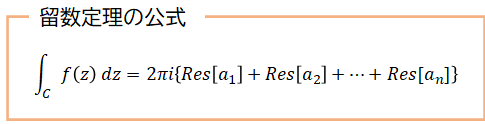
留数定理を証明します!

留数定理の証明
まず、ある関数$f(z)$が、閉曲線$C$内に孤立特異点$a_1,a_2, \cdots ,a_n$を持つとします。(図には3つの孤立特異点しかありませんが、$n$個の孤立特異点があると考えてください。)

次に、孤立特異点を中心とする円$C_1,C_2, \cdots ,C_n$を考えます。
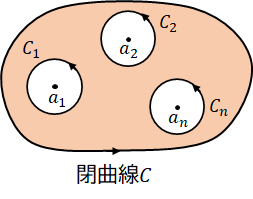
そして、閉曲線$C$から各円に対して切り込みを入れます。

ここで、$f(z)$は孤立特異点$a_1,a_2, \cdots ,a_n$を除く$C$の内部で正則なので、コーシーの積分定理より、
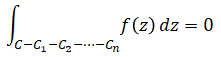
となります。切れ込み部分の線積分は互いに打ち消し合うことに注意しましょう。したがって、
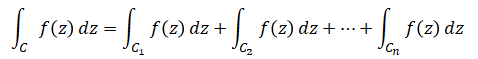
となる。「留数とは?求め方も分かりやすく解説!」の記事で詳しく述べているのですが、特異点$a_i$が存在する関数$f(z)$の閉曲線$C_i$に沿った線積分は、留数$Res[a_i]$を使って、
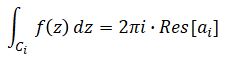
となるから、これを1つ前の式の右辺に適用すると、留数定理の公式が導かれる。

例題
実際に例題を使って留数定理の使い方を確認しましょう。
$|z|=3$の円を積分経路$C$とするとき、次の積分を計算せよ。
$$\displaystyle \int_{C} \frac{z^2}{(z-1)(z-2)} dx$$
解答の最初で
$f(z)=\frac{g(z)}{(z-a)^i}$であるとき、$g(z)$が$z=a$で正則で$g(z) \neq 0$ならば、特異点$z=a$は$k$位の極である
という定理を利用しているので注意してください。今回は$f(z)=\frac{\frac{z^2}{z-2}}{z-1}$と$f(z)=\frac{\frac{z^2}{z-1}}{z-2}$という2パターンにおいて、その定理を利用しました。
$f(z)=\frac{z^2}{(z-1)(z-2)}$は$z=1,2$の2つの1位の極を持ち、どちらも円$C$内に存在する。
$z=1$における留数、$z=2$における留数はそれぞれ、
$$\begin{eqnarray} Res[1]=\displaystyle \lim_{ z \to 1 } (z-1)f(z)
&=& \displaystyle \lim_{ z \to 1 } \frac{z^2}{z-2} \\
&=& -1
\end{eqnarray}$$
$$\begin{eqnarray} Res[2]=\displaystyle \lim_{ z \to 2 } (z-2)f(z)
&=& \displaystyle \lim_{ z \to 2 } \frac{z^2}{z-1} \\
&=& 4
\end{eqnarray}$$
よって、留数定理より、
$$\begin{eqnarray} \displaystyle \int_{C} \frac{z^2}{(z-1)(z-2)} dx
&=& 2\pi i \{ Res[1]+Res[2] \} \\
&=& 2\pi i \cdot (1+4) \\
&=& 10\pi i
\end{eqnarray}$$

パッと見難しそうな積分なのに、簡単に解けちゃったっす!
これが留数定理の力です!

留数定理の凄いところ

複素積分が簡単に出来るのは分かったけど、だからどうしたって感じなんだよね~
留数定理の本当に凄いところは「実積分にも応用できて、普通に実積分を解くよりもかなり早く解ける場合がある」ということなんです!

例えば、$\displaystyle \int_{0}^{ \infty } \frac{1}{x^6+1} dx$という積分はそのまま解こうとすると、部分分数分解を使って延々と地道なことをしないといけません。
でも、留数定理を使うと、かなり楽に解くことが出来てしまうのです。楽と言っても実積分よりは楽なだけで、結構大変ですけどね。
詳しく説明しようとするとかなり大変なので、これ以上はこの記事では書きません。とにかく、「留数定理を使えば実積分が楽になるときがある」とだけ覚えておけば良いでしょう。
今回のまとめ
・留数定理は「閉曲線$C$に沿った周回線積分の値が、$C$内部の全ての 孤立特異点における留数の和に$2\pi i$をかけたものになる」という定理
$$\displaystyle \int_{C} f(z) dx = 2\pi i \{ Res[a_1]+Res[a_2]+ \cdots +Res[a_n] \}$$
・「実積分にも応用できて、普通に実積分を解くよりもかなり早く解ける場合がある」のが留数定理の凄いところ












・留数定理は「閉曲線$C$に沿った周回線積分の値が、$C$内部の全ての 孤立特異点における留数の和に$2\pi i$をかけたものになる」という定理
$$\displaystyle \int_{C} f(z) dx = 2\pi i \{ Res[a_1]+Res[a_2]+ \cdots +Res[a_n] \}$$
・「実積分にも応用できて、普通に実積分を解くよりもかなり早く解ける場合がある」のが留数定理の凄いところ